VolumeVLEGas L3
Created Monday 22 October 2012
Basic two-zone model taking into account heat and mass storage as well as convective heat transfer and pressure differences due to friction and geostatic effects for each of the zones. Variable number of inlet and outlet ports.
1. Purpose of Model
The model is recommended in case that two distinct phases (gas and liquid) are present and no mass transfer between the phases is expected. The gas phase is expected to be always gaseous while the VLE phase may be subcooled, superheated and in the two-phase region. However, the model's common application case is a storage tank somehow connected to the atmosphere.
2. Level of Detail, Physical Effects Considered and Physical Insight
2.1 Level of Detail
Referring to Brunnemann et al. [1], this model refers to the level of detail L3 because the system is modelled with the use of balance equations for two distinct zones, namely the zone of liquid and gas volume.
2.2 Physical Effects Considered
- Conservation of Mass
- Simplified conservation of momentum (no advection term, steady state)
- Conservation of Energy
- Reverse flow
- Heat Transport due to convection
- Pressure loss due to friction.
- heat transfer between the phases (but no mass transfer between the phases)
2.3 Level of Insight
Heat Transfer
- ControlVolumes:Fundamentals:HeatTransport:VLE HT:Constant L3 ypsDependent
- ControlVolumes:Fundamentals:HeatTransport:Generic HT:IdealHeatTransfer L3
Pressure Loss
- ControlVolumes:Fundamentals:PressureLoss:Generic PL:LinearParallelZones L3
- ControlVolumes:Fundamentals:PressureLoss:Generic PL:NoFriction L3
- ControlVolumes:Fundamentals:PressureLoss:Generic PL:LinearSerialZones L3
Spacial Distribution
- Basics:ControlVolumes:Fundamentals:SpatialDistributionAspects:RealSeparated
- ControlVolumes:Fundamentals:SpatialDistributionAspects:RealMixed
3. Limits of Validity
- Averaging assumption within the zonal volumes violated.
- The equations imply that the outlet states are equal to the states in the balance equations - Not true for large volumes and high gradients.
4. Interfaces
4.1 Physical Connectors
Basics:Interfaces:FluidPortIn inlet[geo.N_inlet] - an arbitrary number of inlet ports
Basics:Interfaces:FluidPortOut outlet[geo.N_inlet] - an arbitrary number of outlet ports
Basics:Interfaces:HeatPort a heat
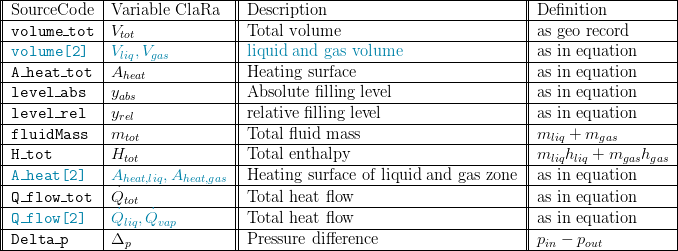
5. Nomenclature
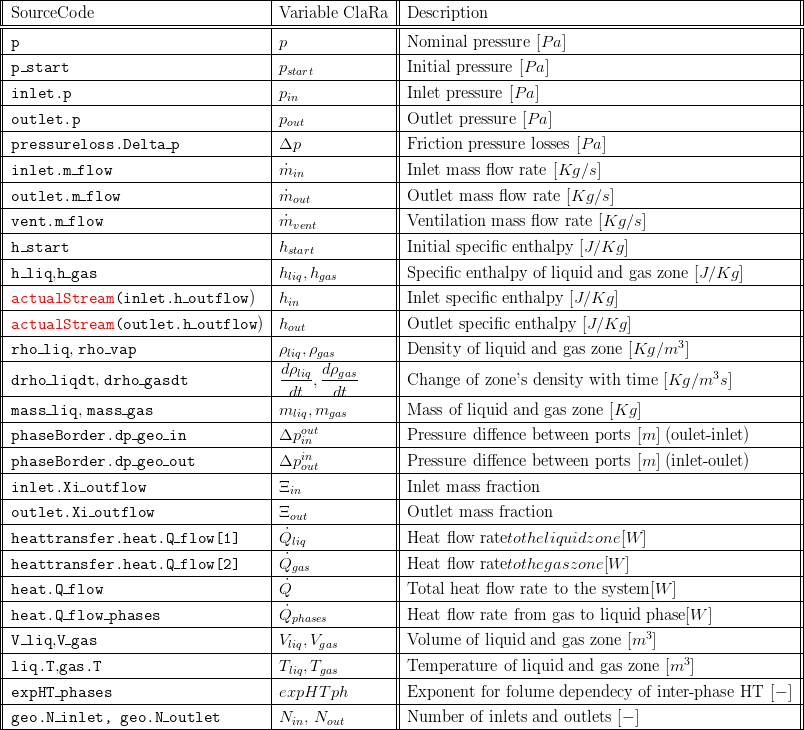
6. Governing Equations
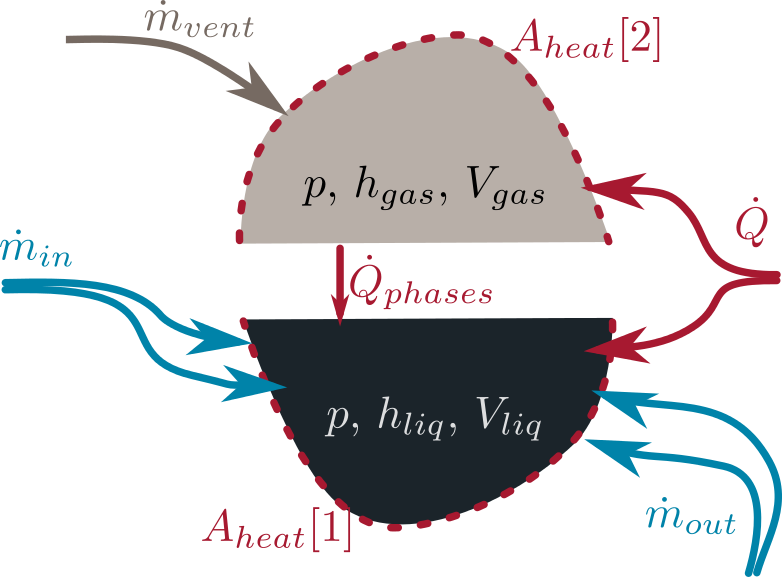
6.1 System Description and General model approach
The general model structure is defined as illustrated below: Two distinct volumes are considered referring to the liquid and gas volume in the system. The two volumes can exchange heat between each other but no mass, i.e. there is no evaporation or condensation. Furthermore, heat can be transferred with the surrounding which is handled using replaceable models, see section 2.3 Heat Transfer. Pressure losses are also addressed with replaceable models, see section 2.3 Pressure Loss. The entering and outgoing enthalpy flows are allocated according to the respective media, i.e. the vent mass flow is allocated to the gas medium while inlet and outlet VLE mass flows are allocated to the liquid volume.
6.2 Governing Model Equations
Conservation of Mass
The mass balance for each of the zones considers evaporation and condensation mass flow rates, volume changes and mass flows through the inlet and outlet connectors. These mass flows are allocated to the vapour and liquid zone according to the replaceable model PhaseSeparation, see section 2.3 Spatial Distribution. The balance equations read:
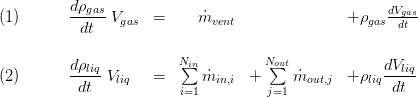
Conservation of Momentum
The momentum balances applied for each of the ports allow a calculation of a pressure distribution at the model boundaries. Two major simplifications are applied:
- steady state
- neglect of momentum flows through the ports
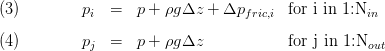
Conservation of Energy
The energy balances for both zones consider entering and leaving enthalpy flow rates as well as energy transport between the zones due to heat and mass transfer. The mass flows entering and leaving are allocated to the vapour and liquid zone according to the replaceable model PhaseSeparation, see section 2.3 Spatial Distribution. Please note, there are three terms in the equations below that take the derivatives of volume, density and pressure into account. These terms are derived from the total derivative of the inner energy of the zone and appear here due to the special choice of state variables as discussed in Basic Concepts of Modelling
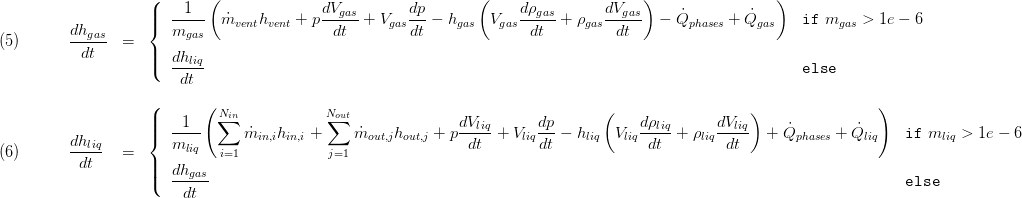
In the above equations two cases are distinguished to handle vanishing zones, i.e. if we have only liquid or only gas in our component. In these cases the enthalpy of vanishing zone follows the other remaining zone's enthalpy. This concept allows to simulate completely filled or void tanks. The heat flow rates to the surrounding are determined by applying a replaceable heat transfer model, see section 2.3 Heat Transfer.
The model's density is taken as an explicit function of the states. Its total derivative should be used for completeness of the model given by:

Chemistry
No chemical reactions are considered leading to the following 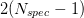 species mass balances for the two zones. Note that these equations are only valid (and evaluated) when a mixture of fluids is used, i.e. the number of species
species mass balances for the two zones. Note that these equations are only valid (and evaluated) when a mixture of fluids is used, i.e. the number of species 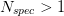 . In case of vanishing zones the derivatives of the mass fractions become zero.
. In case of vanishing zones the derivatives of the mass fractions become zero.
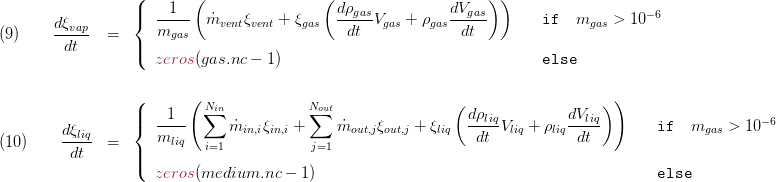
Mass Transfer between the Zones
Evaporation and condensation is not supported, i.e. there is no mass transfer between the two zones.
Heat Transfer between the Zones
The model for the inter-phase heat transfer assumes constant values for heat phase surface and heat transfer coefficient:
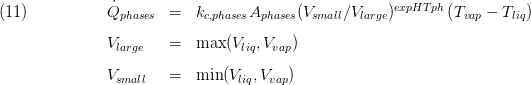
Summary
A summary is available including the following:
- an outline record:
- Basics:Records:FlangeVLE inlet[N_inlet], outlet[N_outlet]
- Basics:Records:FlangeGas vent
- Basics:Records:FluidVLE L34 fluid
7. Remarks for Usage
This model is applied in a number of component models either via instantiation of inheritance, see Components:MechanicalSeparation:BalanceTank L3.
9. References
[1] Johannes Brunnemann and Friedrich Gottelt, Kai Wellner, Ala Renz, André Thüring, Volker Röder, Christoph Hasenbein, Christian Schulze, Gerhard Schmitz, Jörg Eiden: "Status of ClaRaCCS: Modelling and Simulation of Coal-Fired Power Plants with CO2 capture", 9th Modelica Conference, Munich, Germany, 2012
[2] Sebastian Meinke and Friedrich Gottelt, Martin Müller, Egon Hassel: "Modeling of Coal-Fired Power Units with ThermoPower Focussing on Start-Up Process", 8th Modelica Conference, Dresden, Germany, 2011
10. Authorship and Copyright Statement for original (initial) Contribution
Author:
DYNCAP/DYNSTART development team, Copyright 2011 - 2022.
Remarks:
This component was developed during DYNCAP/DYNSTART projects.
Acknowledgements:
ClaRa originated from the collaborative research projects DYNCAP and DYNSTART. Both research projects were supported by the German Federal Ministry for Economic Affairs and Energy (FKZ 03ET2009 and FKZ 03ET7060).
CLA:
The author(s) have agreed to ClaRa CLA, version 1.0. See https://claralib.com/pdf/CLA.pdf
By agreeing to ClaRa CLA, version 1.0 the author has granted the ClaRa development team a permanent right to use and modify his initial contribution as well as to publish it or its modified versions under the 3-clause BSD License.
11. Version History
Date - Version - Description of changes - author/revisor
25.06.2013 - v0.1 - initial implementation of the model - Friedrich Gottelt, XRG Simulation
21.12.2015 - v0.2 - updated species balances covering vanishing zones - Friedrich Gottelt, XRG Simulation
04.05.2017 - v1.2.2 - fixed bug in summary for expertSummary==true - Timm Hoppe, XRG Simulation
Backlinks: ClaRa:Components:MechanicalSeparation:BalanceTank L3
