VolumeGas L2
Created Thursday 18 July 2013
Basic model of a gas volume with dynamic energy and mass balances, taking convective heat transfer and pressure losses into account.
1. Purpose of Model
The model is used as a basic model to form various components which handle gaseous media.
2. Level of Detail, Physical Effects Considered and Physical Insight
2.1 Level of Detail
Referring to Brunnemann et al. [1], this model refers to the level of detail L2.
2.2 Physical Effects Considered
- Conservation of Mass
- Conservation of Energy
- Reverse flow
- Heat Transport due to convection
- Pressure loss due to friction
2.3 Level of Insight
Heat Transfer
- ControlVolumes:Fundamentals:HeatTransport:Generic HT:Adiabat L2
- ControlVolumes:Fundamentals:HeatTransport:Generic HT:IdealHeatTransfer L2
- ControlVolumes:Fundamentals:HeatTransport:Generic HT:Constant L2
- ControlVolumes:Fundamentals:HeatTransport:Generic HT:CharLine L2
Pressure Loss
- ControlVolumes:Fundamentals:PressureLoss:Generic PL:NoFriction L2
- ControlVolumes:Fundamentals:PressureLoss:Generic PL:LinearPressureLoss L2
- ControlVolumes:Fundamentals:PressureLoss:Generic PL:QuadraticNominalPoint L2
Geometry
- Generic_Geometry : Generic geometry
- HollowBlock : Geometry of a hollow block
- HollowBlockWithTubes : Geometry of a hollow block with tubes inside
- Pipe_Geometry : Geometry of a pipe
3. Limits of Validity
- Steady flow.
- Fixed control volume.
- Averaging assumption violated.
- The equations imply that the outlet states equal the states in the balance equations - Not true for large volumes and high gradients.
4. Interfaces
4.1 Physical Connectors
Basics:Interfaces:GasPortIn inlet
Basics:Interfaces:GasPortOut outlet
Basics:Interfaces:HeatPort a heat
4.2 Medium Models
- Gas Medium Model at the inlet and outlet port and inside the volume.
5. Nomenclature
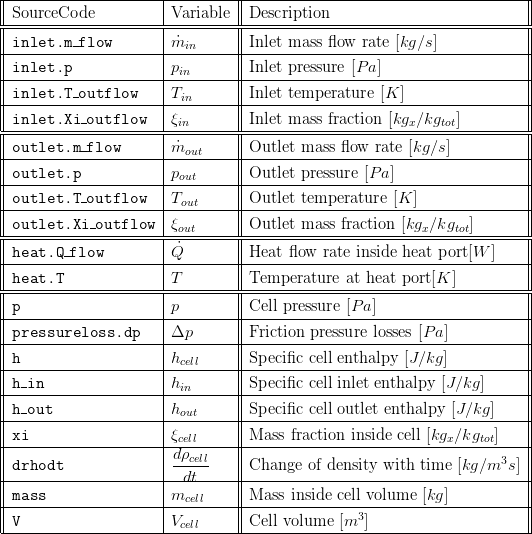
6. Governing Equations
6.1 System Description and General model approach
The model describes an ideally stirred volume element with heat transfer to the surrounding.
6.2 Governing Model Equations
Conservation of Mass
Via parameter preset the user can determine whether the mass balance is calculated dynamic or static. The dynamic mass balance is calculated as follows:
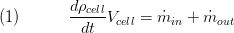
and the static mass balance:
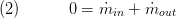
Conservation of Momentum
We use balance of stationary momentum to model the pressure losses on the control volume. The friciton pressure losses are calculated with the replaceable pressure loss models. In the model the pressure distribution is given by the influence of friction in the x direction, which is given with the direction of the flow. The friction pressure loss is lumped at the inlet to avoid direct coupling of two flow models.
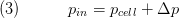
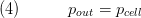
Conservation of Energy
The energy balance considers ingoing and outgoing enthalpy flow rates as well as energy transport to the surrounding (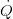 ). Please note the special structure of the energy balance with the differences of ingoing and outgoing enthalpies and the cell enthalpy and the additional term for the pressure derivative which is derived from the total derivative of the inner energy of the cell. The structure results from to the special choice of state variables as discussed in Basic Concepts of Modelling.
). Please note the special structure of the energy balance with the differences of ingoing and outgoing enthalpies and the cell enthalpy and the additional term for the pressure derivative which is derived from the total derivative of the inner energy of the cell. The structure results from to the special choice of state variables as discussed in Basic Concepts of Modelling.
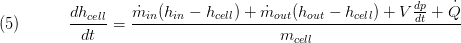
The model's density is taken as an explicit function of the states its total derivative should be used for completeness of the model given by:
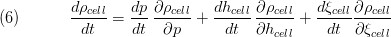
while for stationary energy balance the following equation is used:
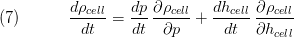
Conservation of Gas Components
The composition is a vector of the component mass fractions. The calculation of the outlet composition depends on the type of mass conservation. If the dynamic mass balance is used, the outlet composition is calculated as follows:
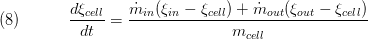
while for static mass balance the following equation is used:
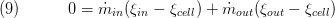
Summary
A summary record is available which bundles important component values.
7. Remarks for Usage
This model is applied in a number of component models either via instantiation of inheritance.
8. References
[1] Johannes Brunnemann and Friedrich Gottelt, Kai Wellner, Ala Renz, André Thüring, Volker Röder, Christoph Hasenbein, Christian Schulze, Gerhard Schmitz, Jörg Eiden: "Status of ClaRaCCS: Modelling and Simulation of Coal-Fired Power Plants with CO2 capture", 9th Modelica Conference, Munich, Germany, 2012
9. Version History
Date - Version - Description of changes - author/revisor
25.06.2013 - v0.1 - initial implementation of the model - André Thüring, TLK-Thermo GmbH
Backlinks: ClaRa:Components:HeatExchangers:HEXvle2gas L3 1ph BU simple ClaRa:Components:HeatExchangers:HEXvle2gas L3 2ph BU simple ClaRa:Basics:ControlVolumes:GasVolumes:Volume Gas L2 advanced ClaRa:Components:FlueGasCleaning:Denitrification:Denitrification L2 ClaRa:Components:FlueGasCleaning:Desulfurization:Desulfurization L2 ideal ClaRa:Components:FlueGasCleaning:E-Filter:E-Filter L2 detailed ClaRa:Components:FlueGasCleaning:E-Filter:E-Filter L2 empirical ClaRa:Components:FlueGasCleaning:E-Filter:E-Filter L2 simple
