ThermoRoot
Created Montag 06 Juni 2016
Square root function linearised around zero and valid for negative inputs
1. Purpose of Function
A typical use case is in pressure loss applications where the velocity is a function of the square root of the pressure difference.
In such cases the usage of the normal square root function has two disadvantages:
- it is only defined for positive arguments → if flow reversal occurs, it cannot handle negative signs of pressure difference
- it has infinite gradient at zero mass flow → at small pressure differences numerical instabilities occur
The function ThermoRoot overcomes these difficulties:
- flow reversal can be handled due to symmetry property of ThermoRoot (see section 5)
- for small arguments ThermoRoot interpolates the square root by a third order polynomial with finite gradient at zero. Close to zero this corresponds to a linear pressure loss model . The third order polynomial is used in order to keep the function and its derivative continous at the boundaries of the interpolation region (see section 5).
2. Limits of Validity
For ThermoRoot and its derivative ThermoRoot_der the interpolation interval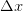 
is assumed to be constant.
It must not change with time.
The width of the interpolation interval shall be small compared to the typical ranges of the argument.
E.g. in pressure loss applications, the interpolation interval width shall be small compared to the nominal pressure loss.
3. Interfaces
4. Nomenclature
5. Governing Equations
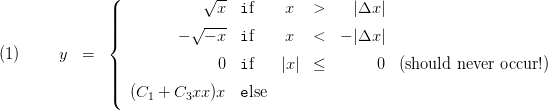
where
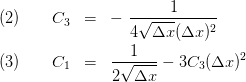
The idea is to interpolate the two square root branches 
and 
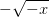by a third order polynomial
whenever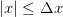 
.
By inspection we see from (1) that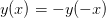 
for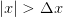 
and hence we must set 
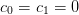in order to keep this symmetry property within the interpolated region.
By demanding continuity of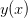 
and its derivative 
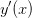at the boundaries 
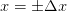we can determine the remaining coefficients as given in (2) and (3).
The resulting function is shown in red in the following plot ( compared to a linear interpolation in blue and the function with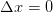 
in green):
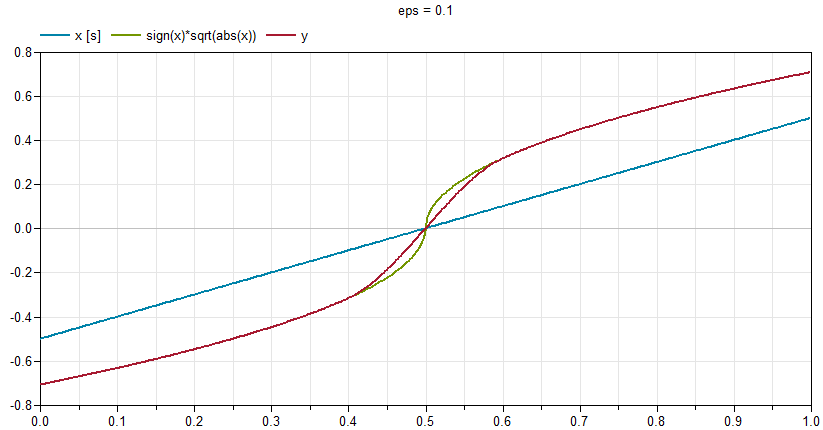
6. Remarks for Usage
7. Validation
8. References
9. Version History
19.07.2011 - v 1.0 - initial implementation - J.Brunnemann/F.Gottelt, XRG Simulation
Backlinks: ClaRa:Basics:Functions:ThermoRoot