QuadraticPressureLoss Simple L4
Created Thursday 08 October 2015
A quadratic pressure drop model - depending on nominal values of pressure difference and mass flow rate, the density and the square root of the actual pressure difference
1. Purpose of Model
This model is appropriate if a pressure drop due to friction, depending on the load is needed (either due to numerical or technical reasons). The model is parametrized by choosing a nominal point and the corresponding pressure loss. A realistic behavior in operating points further away from the nominal point can be expected. The density is taken into account.
2. Physical Insight
This replaceable model is compatible to models of level of detail L4 according to Brunnemann et al. [1] since the friction losses are lumped over the component. The model is regularized around zero, to avoid numerical instability in that point.
3. Limits of Validity
- no supercritical flow conditions are supported
- only in completely developed turbulent flow with rough surfaces the friction factor is independent of the Reynolds number
4. Interfaces
The model communicates via outer models and records. Thus, it expects to have:
- an outer record named iCom as defined in Basics:Records:IComBase L3
- an outer model named geo as defined Fundamentals:Geometry:GenericGeometry
- an inCon record required for communication with FluidDissipation functions
- an inVar record required for communication with FluidDissipation functions
5. Nomenclature
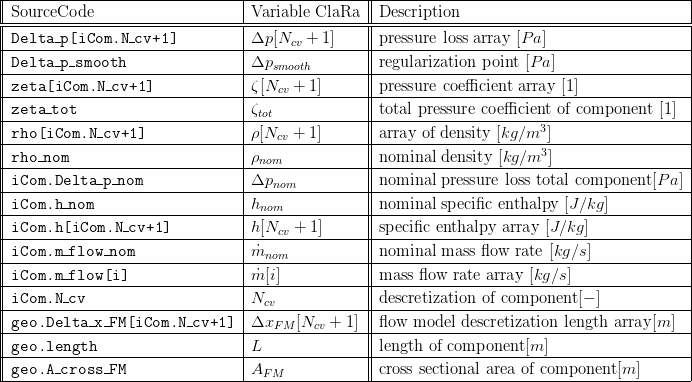
6. Governing Equations
This pressure loss model bases on the QuadraticPressureLoss_L2 model.
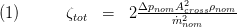
The user can choose between four different flow models for this pressure loss model. This results in four cases:
(a) no pressure loss at inlet, no pressure loss at outlet
(b) no pressure loss at inlet, pressure loss at outlet
(c) pressure loss at inlet, no pressure loss at outlet
(d) pressure loss at inlet, pressure loss at outlet
The pressure coefficient 
is distributed linearly over the component according to the chosen flow model, see Basic Concepts of Modelling for a detailed description. Thus, the pressure coefficient array 
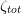is received. The mass flow is calculated by handing over the cross sectional area , the regularization point , the pressure coefficient array and the density array to the FluidDissipation function "dp_pressureLossCoefficient_MFLOW" via communication records.
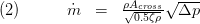
Equation (2) gives the functionality of the FluidDissipation function. See the FluidDissipation documention for more information.
7. Remarks for Usage
The model should be used if huge changes in the load can be expected. The model bases on the quadratic correlation of mass flow rate to pressure loss. Thus, the accuracy in load points which differ significantly from the nominal point is better than in the LinearPressureLoss L2 model.
8. Validation
-
9. References
[1] Johannes Brunnemann and Friedrich Gottelt, Kai Wellner, Ala Renz, André Thüring, Volker Röder, Christoph Hasenbein, Christian Schulze, Gerhard Schmitz, Jörg Eiden: "Status of ClaRaCCS: Modelling and Simulationof Coal-Fired Power Plants with CO2 capture", 9th Modelica Conference, Munich, Germany, 2012
10. Authorship and Copyright Statement for original (initial) Contribution
Author:
DYNCAP/DYNSTART development team, Copyright 2011 - 2022.
Remarks:
This component was developed during DYNCAP/DYNSTART projects.
Acknowledgements:
ClaRa originated from the collaborative research projects DYNCAP and DYNSTART. Both research projects were supported by the German Federal Ministry for Economic Affairs and Energy (FKZ 03ET2009 and FKZ 03ET7060).
CLA:
The author(s) have agreed to ClaRa CLA, version 1.0. See https://claralib.com/pdf/CLA.pdf
By agreeing to ClaRa CLA, version 1.0 the author has granted the ClaRa development team a permanent right to use and modify his initial contribution as well as to publish it or its modified versions under the 3-clause BSD License.
11. Version History
- 2012 - v 0.1 - initial implementation - Friedrich Gottelt, XRG Simulation